Det har vært en del spørsmål (og misforståelser) på forumet her som direkte eller indirekte har dreid seg om Einsteins spesielle relativitetsteori - hovedsakelig angående lysets hastighet og tidsdilatasjon (tidsutvidelse). Av den grunn tenkte jeg å lage en tråd som forklarer denne teorien slik at også de uten vesentlig fysikkbakgrunn kan forstå hva den dreier seg om og hva den innebærer. Forklaringen er hovedsakelig kvalitativ, og målet er at man ikke skal behøve altfor store matematikk- og/eller fysikkunnskaper for å forstå teoriens virkemåte, selv om noe relativt enkel matematikk er benyttet et par steder. De fleste vanlige og viktige begreper og prinsipper innen spesiell relativitet blir forklart. Jeg innser at dette er en "great wall of text", men såpass må man regne med å lese hvis man skal forstå den spesielle relativitetsteorien i noen hensiktsmessig grad. 
Relativitet og referanse
Først og fremst må man være klar over hva relativitet vil si, og hva det innebærer i dagliglivet. Det viktigste er å forstå hvorfor og hvordan fart er relativt. For å forstå det må vi vite hva en referanse er og hvorfor det er viktig. Dette gjøres nok lettest med eksempler.
For å ta det grunnleggende først, se for deg at universet består av kun to legemer i et tomrom. Disse legemene beveger seg vekk fra hverandre med en viss avstand på en viss tid - altså med en konstant fart. Er det da mulig å avgjøre hvem av de som beveger seg og hvem som står stille? Kan man i det hele tatt gi en entydig konklusjon? Man begynner her å se nødvendigheten av å bestemme hva som skal være referansen. Ser man situasjonen fra legeme 1 sitt synspunkt, vil man konkludere med at legeme 2 beveger seg vekk, mens observert fra legeme 2 vil situasjonen være motsatt, og begge deler er like riktig. Det er altså relativt. Vi tar denne tanken med oss videre til et nytt eksempel.
La oss si at du kjører en bil på landeveien. Du holder en fart på 60 km/t, det kommer en bil mot deg i samme fart, langs veien foran deg løper en jogger i 10 km/t i samme retning som deg selv, og i en busk ligger en politimann med radar. Vi har altså fire "legemer" hvor alle har forskjellig fart i forhold til hverandre. Hvis vi starter med å si at politimannen er vår referanse så er det identisk med å si at vi observerer fra politimannens synspunkt, eller at vi velger oss et referansesystem hvor politimannen ikke er i bevegelse. Hva vil politimannen observere? Jo, han vil se akkurat det jeg beskrev tidligere, nemlig to biler i 60 km/t og en jogger i 10 km/t.
Men hva om vi velger deg som observatør, altså et referansesystem hvor du ikke er i bevegelse? Hva observerer vi da? Jo, vi observerer en bil som nærmer seg med 120 km/t, en jogger som nærmer seg med 50 km/t og en politimann som nærmer seg med 60 km/t. Og med joggeren som observatør? Da ser vi en bil som nærmer seg med 50 km/t, altså din bil, en bil som nærmer seg med 70 km/t, og den samme politimannen nærmer seg med 10 km/t. Hastighetene er altså relative, og vi kan faktisk ikke beskrive de før vi har valgt oss et referansesystem. Denne formen for relativitet kalles Galileisk relativitet, eller Galileisk invarians. Dette ble først beskrevet av Galileo Galilei i 1632 gjennom et eksempel med et skip i konstant fart og som ikke gynget på sjøen, hvor det ville være umulig for noen under dekk å bestemme om båten var i bevegelse eller ikke. I etterkant vet man at Galileisk relativitet er en tilnærming til spesiell relativitet og fungerer ved lave hastigheter.
Hva er så "spesielt" med spesiell relativitet?
Den spesielle relativitetsteori blir kalt "den spesielle" fordi den kun gjelder innenfor visse betingelser, i motsetning til den utvidede teorien ved navn "den generelle relativitetsteori". Betingelsene er ganske enkle: Den spesielle relativitetsteori er kun gyldig innenfor referanserammer som er i konstant fart. Med andre ord kan ikke referanserammen akselerere. Men hva betyr det? Akselerasjon er her litt tvetydig, ettersom en referanseramme i fritt fall mot jorden vil endre hastighet sett utenfra, men internt i referanserammen vil du være vektløs og ikke merke noen akselerasjon, og den vil derfor være gyldig. Det vil derfor si at spesiell relativitet er gyldig i de referanserammer hvor alt internt oppfattes som vektløst. Dette blir kalt et treghetssystem fordi Newtons første lov, også kalt treghetsloven, gjelder i systemet. Newtons første lov sier at et legeme som ikke blir utsatt for en kraft vil forbli i ro eller fortsette i en konstant hastighet i en rett linje. Altså, ingen kraft, ingen endring i hastighet hverken i form av fart eller kurs. Du ser kanskje her at begrepet "hastighet" innebærer både fart (så og så mange meter per sekund, for eksempel) og retning. En endring av en av disse er en akselerasjon. Så fort man ikke er vektløs i referanserammen vil altså spesiell relativitet være en tilnærming til generell relativitet, og avviket fra virkeligheten vil avhenge av hvor stor denne kraften er.
Fysikkens lover gjelder over alt
Som tidligere skrevet, konkluderte Galileo Galilei allerede i 1632 at observatørene under dekk ikke kunne bestemme om båten var i bevegelse eller ikke, og dette er et veldig viktig poeng. Nemlig at fysikkens lover er like konsekvente og gyldige i ethvert treghetssystem. Samme hvilken hastighet du beveger deg i, så lenge den er konstant, vil alle de kjente fysikklovene fungere på akkurat samme måte som om du sto stille, nettopp fordi hvorvidt du står stille eller er i bevegelse avhenger av referanserammen din. Ingen referanseramme eller observatør er altså "favorisert" over noen andre.
Lysets hastighet, c
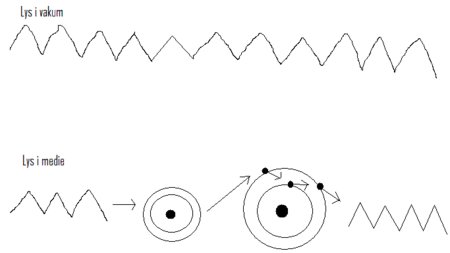
Ut fra fire relativt kompliserte likninger kom James Clerk Maxwell frem til at elektromagnetisk stråling har en hastighet på 299 792 458 m/s (som regel referert til som c), altså nesten 3·10⁸ m/s eller 300 m/µs (µs = mikrosekund). Men så kommer et veldig viktig spørsmål. 300 m/µs, greit nok, men i forhold til hva? Som vi har sett over her, så er jo all hastighet relativ - hvordan kan det da ha seg at lysets hastighet er så spesifikk? Den umiddelbare, og feilaktige konklusjonen, var at det måtte være i forhold til eteren. Eteren var det de trodde var mediumet som lyset forplantet seg i, og som var overalt i universet, men som vi vet i dag at ikke eksisterer. Denne konklusjonen innebærte at Maxwells likninger ikke var gyldige i alle treghetsrammer, og kunne per definisjon ikke kalles fysiske lover, noe som plaget Einstein.
Kort fortalt fant Einstein ut at svaret på spørsmålet om hva lyset beveger seg 300 m/µs i forhold til nødvendigvis er: Alt. Står du her på jorda vil lyset passere deg i alle retninger i hastighet c (sett bort fra en liten oppbremsing som skyldes atmosfæriske gasser), og står du på en annen planet som beveger seg i en enorm hastighet i forhold til jorda vil lyset passere deg i alle retninger i hastighet c der og. Om du står stille, beveger deg mot, eller beveger deg vekk fra lyskilden, så vil lyset fra kilden fortsatt treffe deg i nøyaktig samme hastighet. Dette virker ulogisk, men det er bevist eksperimentelt at det er riktig.
Nå som vi har stadfestet grunnprinsippene i spesiell relativitet, er på tide med noen eksempler for å se hva slags konsekvenser det vi nå har sett på innebærer.
Eksempel på spesiell relativitet - tidsdilatasjon
Dette er et klassisk eksempel du kan ha sett tidligere. Du befinner deg på et fly i konstant fart og jeg på bakken, og vi ser bort fra den lille gravitasjonskraften som drar i oss begge. Oppe i flyet står du i midtgangen og slipper en ball i gulvet fra to meters høyde, og vi sier for enkelhets skyld at dette fallet tar akkurat ett sekund på stoppeklokken din. Du som observatør vil se at ballen beveger seg to meter på ett sekund, og har en gjennomsnittlig hastighet på 2 m/s. Men når jeg er observatør, så har du en hastighet i forhold til meg på 3200 m/s, noe som vil si at ballen også har en lik hastighet i samme retning. På det ene sekundet har ballen gått to meter i høyderetning, men også 3200 m i lengderetning, noe som gjør at ballen har en mye større hastighet i mitt treghetssystem, og at jeg vil se ballens bevegelse som en \-form. Ettersom farten i høyderetning er så lav i forhold til lengderetningen, så forenkler vi litt og sier at ballen hadde en hastighet på 3200 m/s totalt, sett fra mitt perspektiv, og 2 m/s fra ditt perspektiv. Det har gått like lang tid for oss begge, men farten var forskjellig, fordi avstanden ballen reiste var forskjellig. Or, so it seems.
Hva skjer om vi bytter ut ballen med en laserpenn? Du holder laserpennen to meter over gulvet og lyser rett ned, og vi utfører samme eksperiment. For deg vil tuppen av laserstrålen gå to meter rett ned. Jeg, derimot, vil se en tilsvarende \-form (selvfølgelig verdens smaleste \, ettersom lysets hastighet er så enormt mye større enn flyets, men likevel en \). Det kan kun bety at lyset beveger seg to meter for deg, men to meter og bittelitt for meg. Avstanden lyset bevegde seg var altså forskjellig i ditt system fra mitt system, akkurat som med ballen. Og her kommer kickeren: Ettersom lysets hastighet er lik i alle treghetssystemer, men avstanden var forskjellig i ditt og mitt system, kan det kun bety at tiden vår var forskjellig!
Lyset går like fort i ditt treghetssystem som i mitt, noe som betyr at siden lyset gikk lenger sett fra mitt system måtte hendelsen nødvendigvis tatt lenger tid sett fra mitt ståsted. Ettersom hendelser hos deg ser ut til å ta lenger tid, vil jeg altså observere din tid til å gå saktere enn min egen. Dine sekunder er lengre enn mine sekunder. Men som vi husket er hastighet relativt, slik at i din treghetsramme er det jeg som er i bevegelse, og for deg vil det altså se ut som om det er min tid som går sakte.
At min tid går tregere enn din tid samtidig som at din tid går tregere enn min tid høres først umulig ut, men man må huske på at dette er hvordan jeg vil observere din lokale tid, og hvordan du vil observere min lokale tid. I prinsippet er det ikke mer paradoksalt enn at når vi står langt fra hverandre, vil begge se den andre som mindre enn seg selv. Begge kan jo ikke være mindre enn den andre, men det er snakk om en form for perspektiv i begge tilfeller. Men man kan også få varig tidsforskyvelse, som vi skal se.
Tvillingparadokset
Tvillingparadokset dreier seg om to tvillinger født på samme tid (ok, én etter den andre for å gjøre det enklere for mor) på samme sted. Den ene, kall henne Kari, setter seg i et romskip og fyrer avgårde ut i verdensrommet mens den andre, Knut, blir igjen hjemme. La oss si at Kari akselererer fryktelig fort opp i en hastighet på 0,95·c, eller med andre ord 0,95 lysår per år, og at hun reiser 10 lysår utover før hun snur og reiser tilbake. All endring av fart skjer veldig raskt slik at vi kan tilnærme og si at hun har flydd i 0,95·c hele veien.
Knut regner ut tiden Kari skal være borte som t = 20 lysår/0.95 lysår per år = 21 år. Altså vil Knut være 21 år eldre når Kari kommer tilbake. Men hva med Kari? Knut regner ut Karis tid til å gå saktere enn sin egen, og regner ut at Karis oppfattelse av samme tid vil være sqrt(1-0,95²)·21 år = 6,56 år (det som "21 år" ganges med (egentlig deles på) kalles Lorentz-faktoren, og vi skal se på den etterpå). Altså vil Kari være 14,44 år yngre enn Knut når hun kommer tilbake. Begge oppfatter altså sin egen tid som normal og vanlig, men tiden Kari er borte vil av Knut oppfattes å være 21 år, og av Kari vil den oppfattes å være 6,56 år. Men dette virker ikke paradoksalt - det er ingen logiske brister i dette ressonementet.
Så til paradokset. Pga. relativiteten tenker Kari at fra sitt ståsted er det Knut som først beveger seg vekk med 0,95·c og så nærmer seg med 0,95·c, altså er det Knuts tid som går sakte og ikke Karis. Kari forventer dermed at det er Knut som er 14,44 år yngre enn Kari når hun kommer tilbake. Det er jo umulig at begge skal være yngre enn den andre når de møtes igjen, og det er dette som gjør at det ble kalt et paradoks. Løsningen er at Kari sin referanseramme først ble akselerert opp til 0,95·c, for deretter å bremse ned og snu med en akselerasjon andre vegen, og til slutt bremse en gang til når hun kommer tilbake. Tre ganger har altså referanserammen blitt akselerert, og er følgelig ikke et treghetssystem. Kari tar derfor feil, og Knuts konklusjon er riktig. Kari er 14,44 år yngre enn Knut når hun kommer tilbake. Kari måtte trått til med den generelle relativitetsteorien for å få riktig resultat, og i så tilfelle ville hun selvfølgelig kommet frem til det samme som Knut.
Igjen høres det ut som tull og fantasi, men atter igjen er det bekreftet eksperimentelt ved hjelp av svært nøyaktige klokker.

Relativitet og referanse
Først og fremst må man være klar over hva relativitet vil si, og hva det innebærer i dagliglivet. Det viktigste er å forstå hvorfor og hvordan fart er relativt. For å forstå det må vi vite hva en referanse er og hvorfor det er viktig. Dette gjøres nok lettest med eksempler.
For å ta det grunnleggende først, se for deg at universet består av kun to legemer i et tomrom. Disse legemene beveger seg vekk fra hverandre med en viss avstand på en viss tid - altså med en konstant fart. Er det da mulig å avgjøre hvem av de som beveger seg og hvem som står stille? Kan man i det hele tatt gi en entydig konklusjon? Man begynner her å se nødvendigheten av å bestemme hva som skal være referansen. Ser man situasjonen fra legeme 1 sitt synspunkt, vil man konkludere med at legeme 2 beveger seg vekk, mens observert fra legeme 2 vil situasjonen være motsatt, og begge deler er like riktig. Det er altså relativt. Vi tar denne tanken med oss videre til et nytt eksempel.
La oss si at du kjører en bil på landeveien. Du holder en fart på 60 km/t, det kommer en bil mot deg i samme fart, langs veien foran deg løper en jogger i 10 km/t i samme retning som deg selv, og i en busk ligger en politimann med radar. Vi har altså fire "legemer" hvor alle har forskjellig fart i forhold til hverandre. Hvis vi starter med å si at politimannen er vår referanse så er det identisk med å si at vi observerer fra politimannens synspunkt, eller at vi velger oss et referansesystem hvor politimannen ikke er i bevegelse. Hva vil politimannen observere? Jo, han vil se akkurat det jeg beskrev tidligere, nemlig to biler i 60 km/t og en jogger i 10 km/t.
Men hva om vi velger deg som observatør, altså et referansesystem hvor du ikke er i bevegelse? Hva observerer vi da? Jo, vi observerer en bil som nærmer seg med 120 km/t, en jogger som nærmer seg med 50 km/t og en politimann som nærmer seg med 60 km/t. Og med joggeren som observatør? Da ser vi en bil som nærmer seg med 50 km/t, altså din bil, en bil som nærmer seg med 70 km/t, og den samme politimannen nærmer seg med 10 km/t. Hastighetene er altså relative, og vi kan faktisk ikke beskrive de før vi har valgt oss et referansesystem. Denne formen for relativitet kalles Galileisk relativitet, eller Galileisk invarians. Dette ble først beskrevet av Galileo Galilei i 1632 gjennom et eksempel med et skip i konstant fart og som ikke gynget på sjøen, hvor det ville være umulig for noen under dekk å bestemme om båten var i bevegelse eller ikke. I etterkant vet man at Galileisk relativitet er en tilnærming til spesiell relativitet og fungerer ved lave hastigheter.
Hva er så "spesielt" med spesiell relativitet?
Den spesielle relativitetsteori blir kalt "den spesielle" fordi den kun gjelder innenfor visse betingelser, i motsetning til den utvidede teorien ved navn "den generelle relativitetsteori". Betingelsene er ganske enkle: Den spesielle relativitetsteori er kun gyldig innenfor referanserammer som er i konstant fart. Med andre ord kan ikke referanserammen akselerere. Men hva betyr det? Akselerasjon er her litt tvetydig, ettersom en referanseramme i fritt fall mot jorden vil endre hastighet sett utenfra, men internt i referanserammen vil du være vektløs og ikke merke noen akselerasjon, og den vil derfor være gyldig. Det vil derfor si at spesiell relativitet er gyldig i de referanserammer hvor alt internt oppfattes som vektløst. Dette blir kalt et treghetssystem fordi Newtons første lov, også kalt treghetsloven, gjelder i systemet. Newtons første lov sier at et legeme som ikke blir utsatt for en kraft vil forbli i ro eller fortsette i en konstant hastighet i en rett linje. Altså, ingen kraft, ingen endring i hastighet hverken i form av fart eller kurs. Du ser kanskje her at begrepet "hastighet" innebærer både fart (så og så mange meter per sekund, for eksempel) og retning. En endring av en av disse er en akselerasjon. Så fort man ikke er vektløs i referanserammen vil altså spesiell relativitet være en tilnærming til generell relativitet, og avviket fra virkeligheten vil avhenge av hvor stor denne kraften er.
Fysikkens lover gjelder over alt
Som tidligere skrevet, konkluderte Galileo Galilei allerede i 1632 at observatørene under dekk ikke kunne bestemme om båten var i bevegelse eller ikke, og dette er et veldig viktig poeng. Nemlig at fysikkens lover er like konsekvente og gyldige i ethvert treghetssystem. Samme hvilken hastighet du beveger deg i, så lenge den er konstant, vil alle de kjente fysikklovene fungere på akkurat samme måte som om du sto stille, nettopp fordi hvorvidt du står stille eller er i bevegelse avhenger av referanserammen din. Ingen referanseramme eller observatør er altså "favorisert" over noen andre.
Lysets hastighet, c
Ut fra fire relativt kompliserte likninger kom James Clerk Maxwell frem til at elektromagnetisk stråling har en hastighet på 299 792 458 m/s (som regel referert til som c), altså nesten 3·10⁸ m/s eller 300 m/µs (µs = mikrosekund). Men så kommer et veldig viktig spørsmål. 300 m/µs, greit nok, men i forhold til hva? Som vi har sett over her, så er jo all hastighet relativ - hvordan kan det da ha seg at lysets hastighet er så spesifikk? Den umiddelbare, og feilaktige konklusjonen, var at det måtte være i forhold til eteren. Eteren var det de trodde var mediumet som lyset forplantet seg i, og som var overalt i universet, men som vi vet i dag at ikke eksisterer. Denne konklusjonen innebærte at Maxwells likninger ikke var gyldige i alle treghetsrammer, og kunne per definisjon ikke kalles fysiske lover, noe som plaget Einstein.
Kort fortalt fant Einstein ut at svaret på spørsmålet om hva lyset beveger seg 300 m/µs i forhold til nødvendigvis er: Alt. Står du her på jorda vil lyset passere deg i alle retninger i hastighet c (sett bort fra en liten oppbremsing som skyldes atmosfæriske gasser), og står du på en annen planet som beveger seg i en enorm hastighet i forhold til jorda vil lyset passere deg i alle retninger i hastighet c der og. Om du står stille, beveger deg mot, eller beveger deg vekk fra lyskilden, så vil lyset fra kilden fortsatt treffe deg i nøyaktig samme hastighet. Dette virker ulogisk, men det er bevist eksperimentelt at det er riktig.
Nå som vi har stadfestet grunnprinsippene i spesiell relativitet, er på tide med noen eksempler for å se hva slags konsekvenser det vi nå har sett på innebærer.
Eksempel på spesiell relativitet - tidsdilatasjon
Dette er et klassisk eksempel du kan ha sett tidligere. Du befinner deg på et fly i konstant fart og jeg på bakken, og vi ser bort fra den lille gravitasjonskraften som drar i oss begge. Oppe i flyet står du i midtgangen og slipper en ball i gulvet fra to meters høyde, og vi sier for enkelhets skyld at dette fallet tar akkurat ett sekund på stoppeklokken din. Du som observatør vil se at ballen beveger seg to meter på ett sekund, og har en gjennomsnittlig hastighet på 2 m/s. Men når jeg er observatør, så har du en hastighet i forhold til meg på 3200 m/s, noe som vil si at ballen også har en lik hastighet i samme retning. På det ene sekundet har ballen gått to meter i høyderetning, men også 3200 m i lengderetning, noe som gjør at ballen har en mye større hastighet i mitt treghetssystem, og at jeg vil se ballens bevegelse som en \-form. Ettersom farten i høyderetning er så lav i forhold til lengderetningen, så forenkler vi litt og sier at ballen hadde en hastighet på 3200 m/s totalt, sett fra mitt perspektiv, og 2 m/s fra ditt perspektiv. Det har gått like lang tid for oss begge, men farten var forskjellig, fordi avstanden ballen reiste var forskjellig. Or, so it seems.
Hva skjer om vi bytter ut ballen med en laserpenn? Du holder laserpennen to meter over gulvet og lyser rett ned, og vi utfører samme eksperiment. For deg vil tuppen av laserstrålen gå to meter rett ned. Jeg, derimot, vil se en tilsvarende \-form (selvfølgelig verdens smaleste \, ettersom lysets hastighet er så enormt mye større enn flyets, men likevel en \). Det kan kun bety at lyset beveger seg to meter for deg, men to meter og bittelitt for meg. Avstanden lyset bevegde seg var altså forskjellig i ditt system fra mitt system, akkurat som med ballen. Og her kommer kickeren: Ettersom lysets hastighet er lik i alle treghetssystemer, men avstanden var forskjellig i ditt og mitt system, kan det kun bety at tiden vår var forskjellig!
Lyset går like fort i ditt treghetssystem som i mitt, noe som betyr at siden lyset gikk lenger sett fra mitt system måtte hendelsen nødvendigvis tatt lenger tid sett fra mitt ståsted. Ettersom hendelser hos deg ser ut til å ta lenger tid, vil jeg altså observere din tid til å gå saktere enn min egen. Dine sekunder er lengre enn mine sekunder. Men som vi husket er hastighet relativt, slik at i din treghetsramme er det jeg som er i bevegelse, og for deg vil det altså se ut som om det er min tid som går sakte.
At min tid går tregere enn din tid samtidig som at din tid går tregere enn min tid høres først umulig ut, men man må huske på at dette er hvordan jeg vil observere din lokale tid, og hvordan du vil observere min lokale tid. I prinsippet er det ikke mer paradoksalt enn at når vi står langt fra hverandre, vil begge se den andre som mindre enn seg selv. Begge kan jo ikke være mindre enn den andre, men det er snakk om en form for perspektiv i begge tilfeller. Men man kan også få varig tidsforskyvelse, som vi skal se.
Tvillingparadokset
Tvillingparadokset dreier seg om to tvillinger født på samme tid (ok, én etter den andre for å gjøre det enklere for mor) på samme sted. Den ene, kall henne Kari, setter seg i et romskip og fyrer avgårde ut i verdensrommet mens den andre, Knut, blir igjen hjemme. La oss si at Kari akselererer fryktelig fort opp i en hastighet på 0,95·c, eller med andre ord 0,95 lysår per år, og at hun reiser 10 lysår utover før hun snur og reiser tilbake. All endring av fart skjer veldig raskt slik at vi kan tilnærme og si at hun har flydd i 0,95·c hele veien.
Knut regner ut tiden Kari skal være borte som t = 20 lysår/0.95 lysår per år = 21 år. Altså vil Knut være 21 år eldre når Kari kommer tilbake. Men hva med Kari? Knut regner ut Karis tid til å gå saktere enn sin egen, og regner ut at Karis oppfattelse av samme tid vil være sqrt(1-0,95²)·21 år = 6,56 år (det som "21 år" ganges med (egentlig deles på) kalles Lorentz-faktoren, og vi skal se på den etterpå). Altså vil Kari være 14,44 år yngre enn Knut når hun kommer tilbake. Begge oppfatter altså sin egen tid som normal og vanlig, men tiden Kari er borte vil av Knut oppfattes å være 21 år, og av Kari vil den oppfattes å være 6,56 år. Men dette virker ikke paradoksalt - det er ingen logiske brister i dette ressonementet.
Så til paradokset. Pga. relativiteten tenker Kari at fra sitt ståsted er det Knut som først beveger seg vekk med 0,95·c og så nærmer seg med 0,95·c, altså er det Knuts tid som går sakte og ikke Karis. Kari forventer dermed at det er Knut som er 14,44 år yngre enn Kari når hun kommer tilbake. Det er jo umulig at begge skal være yngre enn den andre når de møtes igjen, og det er dette som gjør at det ble kalt et paradoks. Løsningen er at Kari sin referanseramme først ble akselerert opp til 0,95·c, for deretter å bremse ned og snu med en akselerasjon andre vegen, og til slutt bremse en gang til når hun kommer tilbake. Tre ganger har altså referanserammen blitt akselerert, og er følgelig ikke et treghetssystem. Kari tar derfor feil, og Knuts konklusjon er riktig. Kari er 14,44 år yngre enn Knut når hun kommer tilbake. Kari måtte trått til med den generelle relativitetsteorien for å få riktig resultat, og i så tilfelle ville hun selvfølgelig kommet frem til det samme som Knut.
Igjen høres det ut som tull og fantasi, men atter igjen er det bekreftet eksperimentelt ved hjelp av svært nøyaktige klokker.
Sist endret av Provo; 12. mai 2012 kl. 08:00.